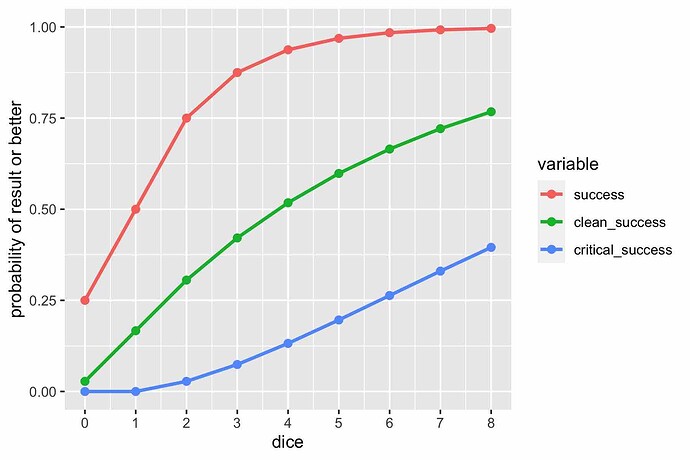
Here’s a table of cumulative probabilities of rolling a partial success or better (4-5+), rolling a clean success or better (6+), and of rolling a critical success (66, representing two 6s in the dice pool).
dice 4-5+ 6+ 66
0 0.250 0.028 0.000
1 0.500 0.167 0.000
2 0.750 0.306 0.028
3 0.875 0.421 0.074
4 0.938 0.518 0.132
5 0.969 0.598 0.196
6 0.984 0.665 0.263
7 0.992 0.721 0.330
8 0.996 0.767 0.395
With six dice, the clean success probability is a nearly 2/3 and the outright failure rate is under 1/60.
Here’s a plot of the same data.
The main takeaway is that each additional die halves the chance of failure, which is 1 minus the probability of rolling 4-5 or better. In a desperate situation where the crew’s outmatched, it makes a lot of sense to take the stress and/or devil’s bargain for another die to cut the probability of failure in half. The chance of a clean success or better goes up much more slowly, with the value (1 - 5/6^N) vs. (1 - 1/2^N) for a success or better. Both ways, the rate of failure decay is exponential.
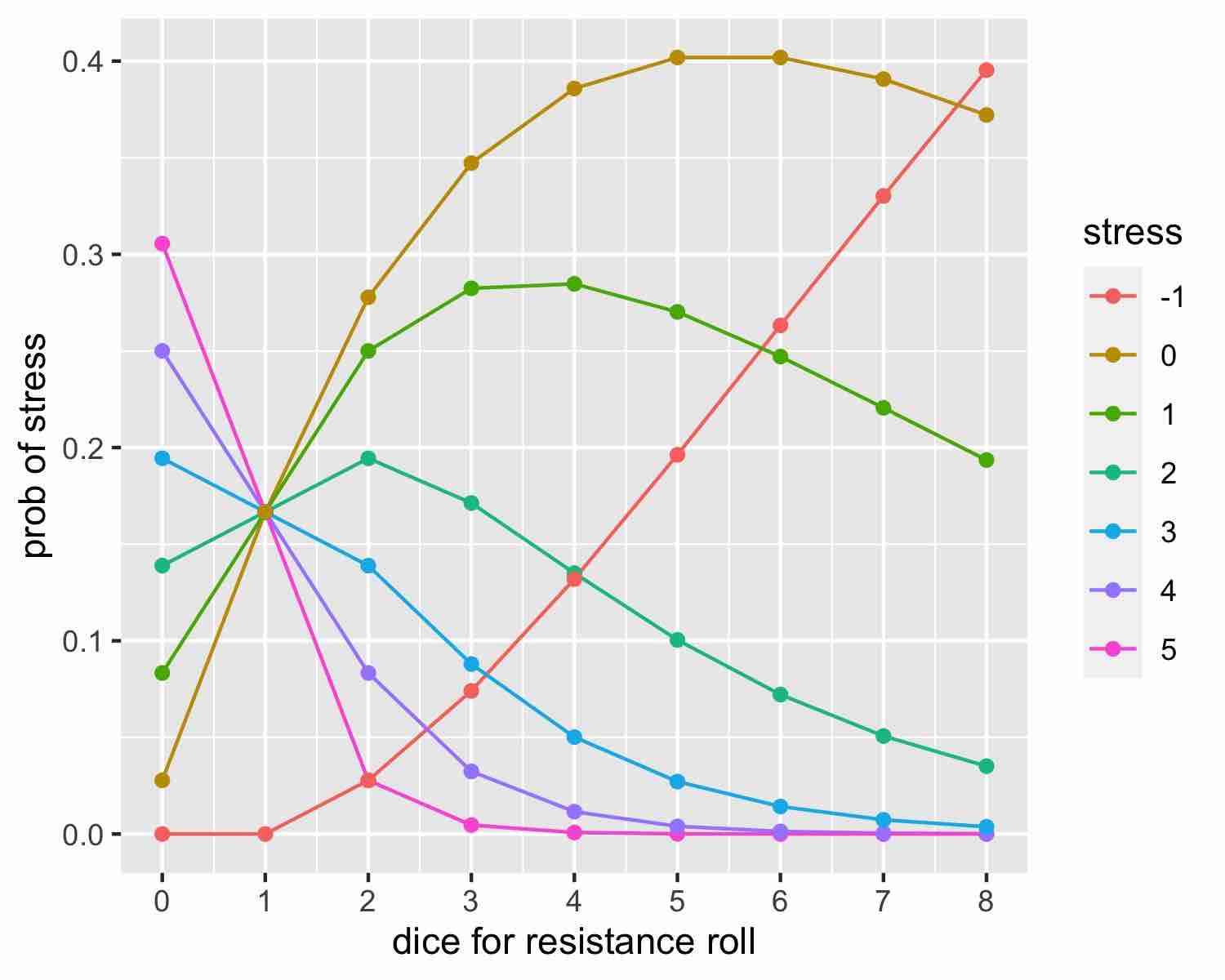
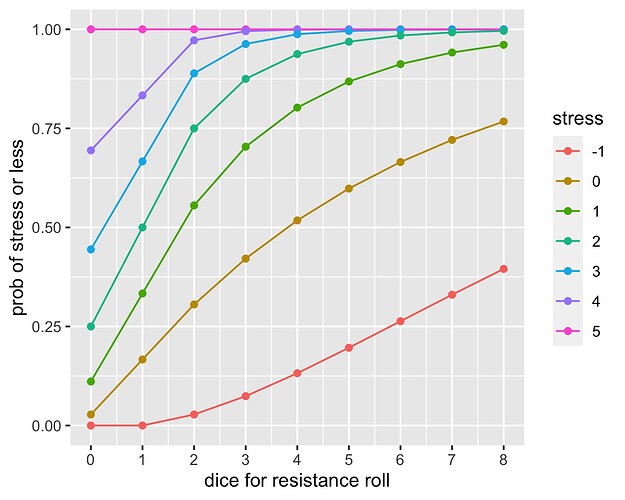
I originally published this analysis in a comment on a blog post, Probabilities for action and resistance in Blades in the Dark. I’m a computational statistician by day, RPG-er by night. That includes the actual probabilities of different resistance rolls vs. dice pool. I should probably put that into a cumulative plot, too, so that players can easily assess the probabilty of overindulging their vice (as both my players’ characters did out of the gate because they had at least 1 dot in every attribute trying to cover all the bases as a two-man crew).
Here’s some crude R code to generate the plots and table. My excuse is that I’m a C++ programmer, not an R programmer. It’s probably possible to do this via AnyDice, but I don’t know their language. The dynamic programming algorithm to compute the probabilities was cribbed from Bouke van der Spoel’s comment on my original blog post. The recursion neatly illustrates how adding one more die updates the probabilities. It also illustrates how the failure rates drop exponentially because of the multiplications.
library('ggplot2')
library('reshape')
res <- matrix(NA, nrow = 8, ncol = 4)
# 1-8 dice case with base case followed by recursion
res[1, 1:4] <- c(3/6, 2/6, 1/6, 0)
for (n in 2:8) {
res[n, 1:4] <- c(res[n - 1, 1] * 3/6,
res[n - 1, 1] * 2/6 + res[n - 1, 2] * 5/6,
res[n - 1, 1] * 1/6 + res[n - 1, 2] * 1/6 + res[n - 1, 3] * 5/6,
res[n - 1, 3] * 1/6 + res[n - 1, 4])
}
# bind in special case for 0 dice, now indexed 1-9
cumulative_df <-
rbind(data.frame(success = 1/4, clean_success = 1/36, critical_success = 0),
data.frame(success = res[ , 2] + res[ , 3] + res[ , 4],
clean_success = res[ , 3] + res[ , 4],
critical_success = res[ , 4]))
# convert to long form for plotting using reshape::melt, add number of dice values
long_df <- cbind(dice = c(0:8, 0:8, 0:8), melt(cumulative_df))
# generate plot and save as jpg
plot <- ggplot(long_df, aes(x = dice, y = value, colour = variable)) +
geom_point(size = 2) +
geom_line(size = 1) +
ylab("probability of result or better") +
scale_x_continuous(breaks = 0:8) +
scale_y_continuous(breaks = c(0, 0.25, 0.5, 0.75, 1.0),
lim = c(0, 1))
ggsave('bidt-cumulative-action-probs.jpg', width = 7, height = 4)
# print table with 3 decimal places of accuracy
cat(sprintf("%5s %5s %5s %5s\n", "dice", "4-5+", "6+", "66"))
for (n in 1:9)
cat(sprintf("%5d %5.3f %5.3f %5.3f\n", n - 1,
cumulative_df[n, 1], cumulative_df[n, 2], cumulative_df[n, 3]))